What is twist and ply?
When choosing a yarn it is important to consider the twist and ply as this affects how the yarn behaves.
Twisting yarn is the process of wrapping together (in a spiral motion) fibres to make a singles yarn and then singles to make a plied yarn. Twisting fibres together, such as when spinning, gives the fibres the strength to be woven in to cloth. Twisting these singles together to make a plied yarn adds even more strength.
The ply of a yarn is the number of singles that have been twisted together to make up a yarn. A single yarn would have a ply of one.
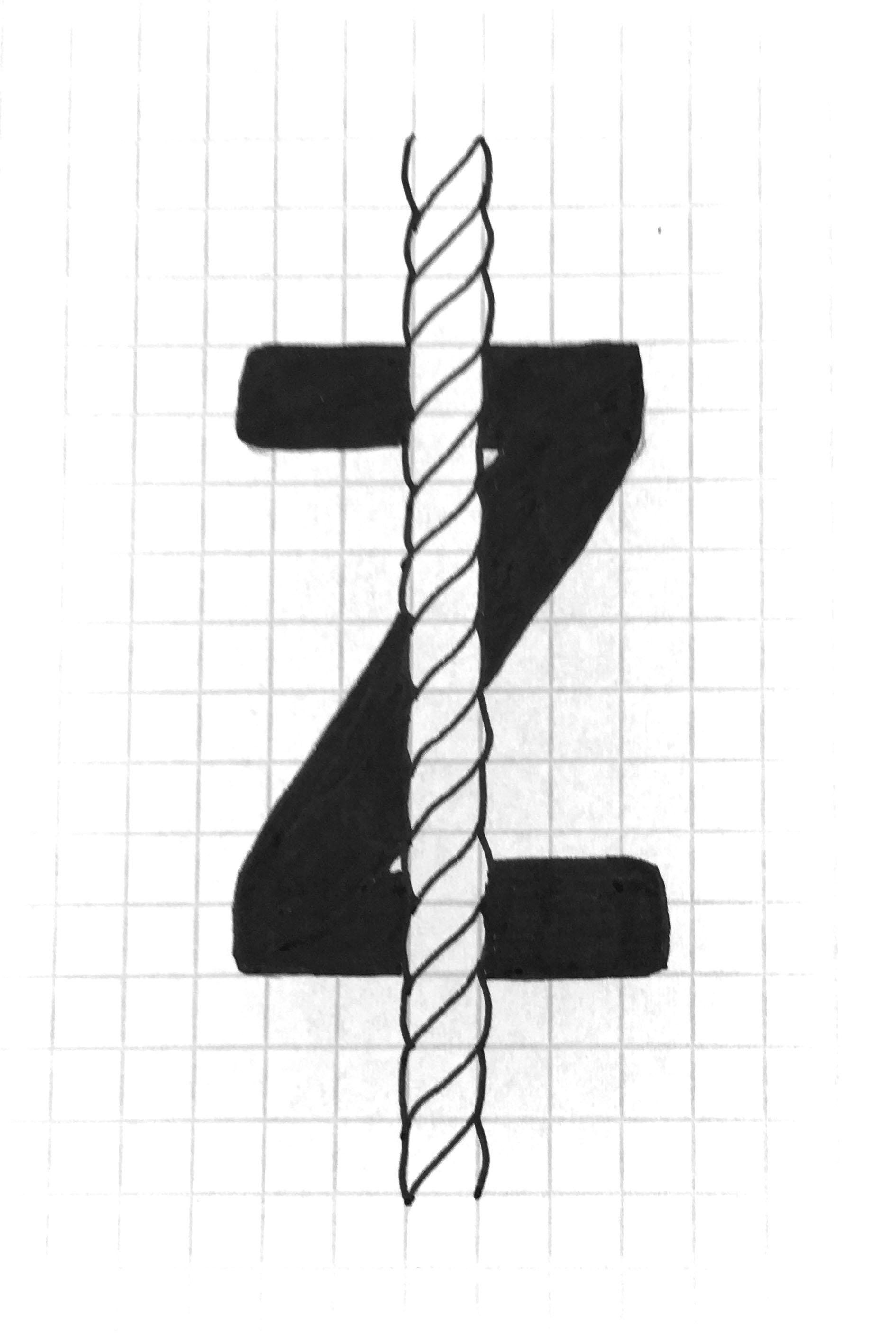
We describe the twist of a yarn as either an ‘S’ or ‘Z’ twist. To determine which way a yarn is twisted, hold the yarn vertically and visualise the diagonal in each of these letters. If the fibres appear
to be going in the same direction as the diagonal in an ‘S’ then it is an ‘S’ twist yarn. If they are going in the opposite direction then it is a ‘Z’ twist yarn.
Why is it important?
When yarn has been plied together the single strands are often ‘Z’ twist yarns which are then plied in an ‘S’ direction. If multiple ply ‘S’ twist yarns are then to be plied together, such as in a cord, they would be twisted in a ‘Z’ direction. Alternating twists in this way gives the yarn stability and strength.
If a yarn is plied together using the same direction twist as the single strands, for example the single strands were twisted in a ‘Z’ direction and the yarn was also plied in the ‘Z’ direction the resulting yarn will have a tendency to curl. This is apparent in fabrics such as voile.
The number of twists per meter is also important. This information is not always given with the yarn as standard but it will be displayed a TMI (twists per metre or TPI twists per inch). Some yarns are highly twisted and have lots of twists per meter while others are more softly twisted with less twists per meter. Shorter staple fibres will need a higher twist than longer staple fibres to give them the strength needed to be woven.
As a yarn’s TPM increases as does it’s strength until it reaches it ‘optimum twist’ (different for every yarn). Optimum twist is when the yarn is at its strongest. If twisted more than this it starts to weaken. weakening the yarn in this way is sometimes necessary to create a desired effect.
How twist and ply is applied
The twist of a singles/yarn defines the characteristics of the yarn:
| Low twist yarns | High twist yarns |
| Softer (produce softer, lighter fabrics) | Smoother, harder and stronger (produce finer, crisper fabrics) |
| Absorbent | Can be water repellent |
| Less hard wearing | More resistant to abrasion and pilling |
| Fabric more relaxed and less likely to curl | Very high twist yarns are lively and the fabric more likely to curl |
It is very important to consider the twist of a yarn when weaving a fabric as this may help us us achieve a desired fabric. These are a few examples of some fabrics in which the twist is very important:
| Fabric | Twist characteristics |
| Crepe | Very highly twisted yarn |
| Voile | Fibre spun in ‘Z’ direction with yarn also spun in ‘Z’ direction. High twist yarn which likes to curl but also creates transparency. |
| Poplin | Yarn which has been spun in an ‘S’ twist using two singles spun in ‘Z’ twists. |
| Herringbone structured fabric | When the yarn twist and direction of the twill structure are in opposite directions the twill will be more prominent e.g. ‘S’ twist yarn with ‘Z’ direction twill |
Sewing thread is made up of three ‘S’ twist singles then plied in a ‘Z’ direction which creates a tear resistant yarn.
Yarn Counts